miércoles, 30 de septiembre de 2020

RESOLUCIÓN DE PROBLEMAS CON POTENCIAS DE NÚMEROS ENTEROS

 VIDEO TUTORIAL3 : Tomado de https://www.youtube.com/watch?v=sSl-hODo8A8

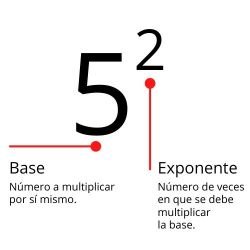
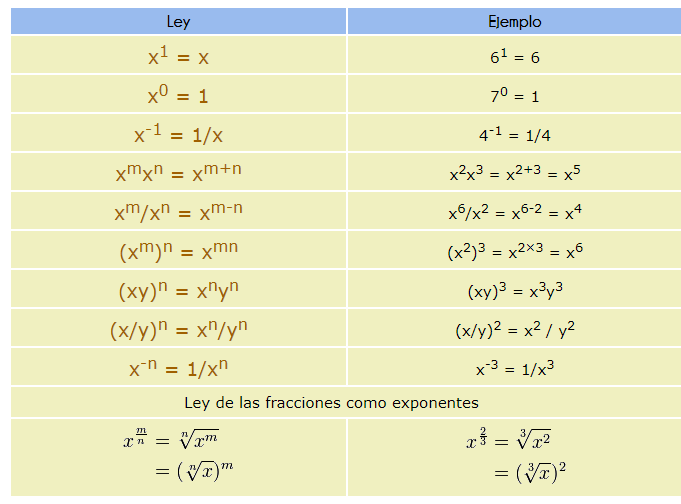
PROBLEMAS CON POTENCIAS

VIDEO TUTORIAL4:  Tomado de https://www.youtube.com/watch?v=7VPpY51LmvA&t=457s

Aplicando potencias ,para resolver problemas de bacterias

Tomado de: https://www.smartick.es/blog/matematicas/algebra/problemas-con-potencias/ 

Problemas con potencias y repaso del concepto

45 Comentarios

¿Conoces las potencias? ¿Sabes para qué y cómo se utilizan? Hoy vamos a ver un ejemplo que te ayudará a resolver los problemas con potencias.


La Hidra de Lerna es un personaje mitológico que aparece en algunas historias, como la de las 12 pruebas de Hércules. La Hidra era un monstruo con 1 cabeza, pero si se le cortaba, le nacían 2 cabezas en su lugar. Si un héroe intentaba vencerla cortándole todas sus cabezas cada día, ¿cuántas cabezas tendría la Hidra el tercer día? ¿y al cabo de 10 días intentando vencerla?

Vamos a resolver la primera pregunta de este problema, pensemos:

  • El primer día, al cortarle una cabeza, el monstruo tenía 2 cabezas
  • El segundo día, al cortarle todas las cabezas, nacieron el doble: 2 x 2 = 4 cabezas
  • El tercer día, volvieron a nacer el doble de cabezas: 2 x 2 x 2 = 8 cabezas
  • En resumen, para saber cuántas cabezas tenía tras estos 3 días, hemos multiplicado 2 tres veces.

Para resolver la segunda pregunta, tendríamos que hacer el mismo procedimiento, pero es un poco largo.

  • Para saber cuántas cabezas tendría el monstruo en 10 días, debemos hacer la siguiente operación:

2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2

  • También es muy largo, ¿verdad? Por eso será más fácil de resolver si utilizamos una potencia, expresando la misma operación del siguiente modo:

210 = 1024 cabezas

¿Qué te parece? ¿Verdad que es más fácil resolver este tipo de problemas si utilizamos las potencias?

Si quieres seguir aprendiendo matemáticas y resolución de problemas, registrate en Smartick y pruéba nuestro método gratis.

EJERCICIOS CON POTENCIACIÓN
Tomado de: Blogger de JULIOPROFE






Publicado por en No hay comentarios:

miércoles, 2 de septiembre de 2020

MULTIPLICACIÓN DIVISIÓN Y POTENCIACIÓN DE NÚMEROS ENTEROS

 

PLANEACIÓN DEPARTAMENTO DE MATEMÁTICAS IETI ANTONIO JOSÉ CAMACHO
Segundo semestre  
Año lectivo 2020.

SÉPTIMO






PENSAMIENTO NUMÉRICO Y SISTEMAS NUMÉRICOS


* Multiplicación, división y potenciación

de  números enteros.

*Números Racionales


PENSAMIENTO ESPACIAL Y SISTEMAS GEOMÉTRICOS

Geometría:  medición

*Figuras planas: Polígonos, Triángulos, cuadriláteros.

PENSAMIENTO MÉTRICO Y SISTEMA DE MEDIDAS

*Áreas
*Perímetros







COGNITIVO


Reconoce   las operaciones multiplicación, división y potenciación de enteros en diferentes contextos


Identifica el conjunto de  los racionales y/o decimales en diferentes contextos.



Comprende los conceptos de  perímetro y área de figuras planas.


PROCEDIMENTAL


Aplica las operaciones multiplicación, división y potenciación de enteros en diferentes contextos.


Aplica el conjunto de  los racionales y/o decimales en diferentes contextos.


Soluciona situaciones de la vida cotidiana en las que se involucran  el perímetro y el  área de figuras planas


ACTITUDINAL


Guarda   y  organiza  la información virtual recibida en el correo electrónico institucional o en un dispositivo  de almacenamiento  propio  para recibir y dirigirla al  docente del área respectiva.


Utiliza de manera adecuada las herramientas tecnológicas (chats, correos, aplicaciones y los recursos para acceder a ellos, cámara, micrófonos).

 

Respeta  al docente  y a sus compañeros del grupo en el uso de la palabra o mensajes por el chat, en las sesiones de interacción por  los medios virtuales que se utilicen en las clases, evitando compartir el link con personas ajenas a la clase. 


Aplica las normas establecidas en la clase de matemáticas para la buena convivencia en los encuentros virtuales. 




MULTIPLICACIÓN  DIVISIÓN  Y POTENCIACIÓN DE NÚMEROS ENTEROS 

Aritmética/Multiplicacion de Números Enteros

Ir a la navegaciónIr a la búsqueda

La multiplicación de números enteros, al igual que la suma, requiere determinar por separado el signo y valor absoluto del resultado.

En la multiplicación (o división) de dos números enteros se determinan el valor absoluto y el signo del resultado de la siguiente manera:

  • El valor absoluto es el producto de los valores absolutos de los factores.
  • El signo es «+» si los signos de los factores son iguales, y «−» si son distintos.


Para recordar el signo del resultado, también se utiliza la regla de los signos:

Definición. * (+) × (+)=(+) Más por más igual a más.

  • (+) × (−)=(−) Más por menos igual a menos.
  • (−) × (+)=(−) Menos por más igual a menos.
  • (−) × (−)=(+) Menos por menos igual a más.

Ejemplos. (+4) × (−6) = −24 , (+5) × (+3) = +15 , (−7) × (+8) = −56 , (−9) × (−2) = +18.

La multiplicación de números enteros tiene también propiedades similares a la de números naturales:

La multiplicación de números enteros cumple las siguientes propiedades:

Ejemplo.

  1. Propiedad asociativa:
  1. [ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140
    (−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140
  2. Propiedad conmutativa:
    (−6) × (+9) = −54
    (+9) × (−6) = −54

La suma y multiplicación de números enteros están relacionadas, al igual que los números naturales, por la propiedad distributiva:

Propiedad distributiva.' Dados tres números enteros , el producto  y la suma de productos  son idénticos.


Ejemplo.

  • (−7) × [ (−2) + (+5) ] = (−7) × (+3) = −21
  • [ (−7) × (−2) ] + [ (−7) × (+5) ] = (+14) + (−35) = −21

VIDEO TUTORIAL1  JULIO PROFE : Multiplicación y división de números enteros.

VIDEO TUTORIAL2: RUBÉN SEBASTIAN:  Operaciones combinadas



POTENCIACIÓN  DE  NÚMEROS ENTEROS

Tomado de: https://sites.google.com/site/angelpuente/los-numeros-enteros/3-14---potencia-de-numeros-enteros

3.14.- Potencia de números enteros

1.- BASE POSITIVA Y EXPONENTE POSITIVO
Ya lo hemos visto puesto que coincide con las potencias de números naturales.

2.- BASE NEGATIVA Y EXPONENTE POSITIVO
No hay ninguna dificultad. Únicamente debemos tener cuidado al multiplicar los signos
negativos.
(− 2)1 = − 2
(− 2)2 = (− 2) ⋅ (− 2) = 4
(− 2)3 = (− 2) ⋅ (− 2) ⋅ (− 2) = − 8
(− 2)4 = (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) = 16
(− 2)5 = (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) = − 32
Regla de los signos:
Cuando la base es negativa y el exponente es par el resultado es positivo.
Cuando la base es negativa y el exponente es impar el resultado es negativo.

3.- BASE POSITIVA Y EXPONENTE NEGATIVO
De acuerdo con la definición inicial de potencia:
4(–3)
consistiría en realizar una multiplicación de 4 por sí mismo tantas veces como diga elexponente, en este caso, –3. Esto, lógicamente, no tiene sentido. En cambio, los matemáticos se han puesto de acuerdo en darle un significado a esta expresión:
En general:
Para explicar este resultado acudimos a la fórmula de la división de potencias de la misma
base:
Pero esto se puede resolver realizando las potencias por separado y simplificando:


Así, para que la fórmula de la división de potencias funcione siempre, se acordó que la potencia de exponente negativo es igual a 1 dividido por la misma potencia pero elevada a exponente positivo.

4.- BASE NEGATIVA Y EXPONENTE NEGATIVO
Es parecido al caso anterior pero ahora la base sigue siendo negativa:


5.- BASE POSITIVA O NEGATIVA Y EXPONENTE CERO
Cualquier número positivo o negativo elevado a exponente 0 es igual a 1.

a0 =1
(− a)0 =1

La justificación de estos resultado se hace a partir de la división de potencias de la misma base:
32 : 32 = 30
Pero también se puede resolver realizando previamente las potencias
32 : 32 = 9 : 9 = 1

Lo mismo ocurre cuando las bases son negativas:
(−2)3 : (−2)3 = (−2)0
(−2)3 : (−2)3 = (−8) : ( −8) = 1



¿Cuáles son las leyes de los exponentes?

Las leyes de los exponentes son el conjunto de reglas establecidas para resolver las operaciones matemáticas con potencias.

La potencia o potenciación consiste en la multiplicación de un número por sí mismo varias veces, y se representan gráficamente de la siguiente manera: xy.

El número que se ha de multiplicar por sí mismo es llamado base y el número de veces por el que se ha de multiplicar es llamado exponente, el cual es más pequeño y debe situarse a la derecha y arriba de la base.

Por ejemplo,

leyes de los exponentes

Ahora bien, en operaciones de suma, resta, multiplicación y división con una o varias potencias, ¿cómo proceder? Las leyes de los exponentes nos guían para resolver estas operaciones de la manera más simple posible. Veamos.

1) Potencia cero

1) Todo número elevado a la 0 es igual a 1.

Por ejemplo,

x0 = 1

50 = 1

370 = 1

2) Potencia a la 1

Todo número elevado a 1 es igual a sí mismo.

Por ejemplo,

x1 = x

301 = 30

451 = 45

3) Multiplicación de potencias con la misma base

El producto de potencias con base idéntica es igual a una potencia de igual base, elevada a la suma de los exponentes.

Por ejemplo,

24 · 22 · 24 = 2(4 + 2 + 4) = 210

4) División de potencias con la misma base

Cuando se dividen potencias con la misma base y exponentes diferentes, el cociente es igual a otra potencia con la misma base elevada a la suma de los exponentes.

Por ejemplo,

44 : 42 = 4(4 - 2) = 42

5) Multiplicación de potencias con el mismo exponente

El producto de dos o más potencias diferentes con igual exponente es igual al producto de las bases elevado al mismo exponente.

Por ejemplo:

32 · 22 · 32 = (3 · 2 · 3)2 = 182

6) División de potencias con el mismo exponente

El cociente entre dos potencias con base diferentes e igual exponente resulta en el cociente de las bases elevado al mismo exponente.

Por ejemplo,

82 : 22 = (8 : 2)2 = 42

7) Potencia de una potencia

La potencia de una potencia resulta en otra potencia con la misma base elevada al producto de los exponentes.

Por ejemplo:

(83)3 = 8(3 · 3) = 89

También te puede interesar Leyes de los exponentes y los radicales.

Ley de los exponentes - Ejercicios Resueltos - Fisimat

EJERCICIOS DE APLICACIÓN

Tomado de  https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/racionales/ejercicios-resueltos-de-potencias.html

Ejercicio 1

Escribe en forma de una sola potencia: Aplicando la Ley de exponentes y escribe el nombre de la propiedad empleada en cada ejercicio.

 

1 3³ · 34 · 3 =                           2 57 : 5³ =                         3 (5³)4 =             

 

4 (5 · 2 · 3)4 =                          5 (34)4 =                            6 [(5³)4]² =

 

7 (8²)³=                                     8 (9³)²=                              9 25 · 24 · 2 =

 

10 27 : 26 =                               11 (2²)4 =                           12 (4 · 2 · 3)4 =

 

13 (25)4 =                                   14 [(2³)4]0=                        15 (27²)5=

 

16 (4³)² =

 

Ejercicio 2

Realizar las siguientes operaciones con potencias:

1 (−2)² · (−2)³ · (−2)4 =                     2 (−8) · (−2)² · (−2)0 (−2) =    

3 (−2)−2 · (−2)³ · .(−2)4 =                   4 2−2 · 2−3 · 24 =

 5 2² : 2³ =                                         6 2−2 : 2³ =

7 2² : 2−3 =                                          8 2−2 : 2−3=

9 [(−2)−2] 3 · (−2)³ · (−2)4 =                   10 [(−2)6 : (−2)³]³ · (−2) · (−2)−4 =

 

 

Ejercicio 3



Publicado por en 2 comentarios:
Suscribirse a: Entradas (Atom)