MULTIPLICACIÓN DIVISIÓN Y POTENCIACIÓN DE NÚMEROS ENTEROS

 

PLANEACIÓN DEPARTAMENTO DE MATEMÁTICAS IETI ANTONIO JOSÉ CAMACHO

Segundo semestre  

Año lectivo 2020.

SÉPTIMO	PENSAMIENTO NUMÉRICO Y SISTEMAS NUMÉRICOS * Multiplicación, división y potenciación de  números enteros. *Números Racionales PENSAMIENTO ESPACIAL Y SISTEMAS GEOMÉTRICOS Geometría:  medición *Figuras planas: Polígonos, Triángulos, cuadriláteros. PENSAMIENTO MÉTRICO Y SISTEMA DE MEDIDAS *Áreas *Perímetros	COGNITIVO Reconoce   las operaciones multiplicación, división y potenciación de enteros en diferentes contextos Identifica el conjunto de  los racionales y/o decimales en diferentes contextos. Comprende los conceptos de  perímetro y área de figuras planas.
		PROCEDIMENTAL Aplica las operaciones multiplicación, división y potenciación de enteros en diferentes contextos. Aplica el conjunto de  los racionales y/o decimales en diferentes contextos. Soluciona situaciones de la vida cotidiana en las que se involucran  el perímetro y el  área de figuras planas
		ACTITUDINAL Guarda   y  organiza  la información virtual recibida en el correo electrónico institucional o en un dispositivo  de almacenamiento  propio  para recibir y dirigirla al  docente del área respectiva. Utiliza de manera adecuada las herramientas tecnológicas (chats, correos, aplicaciones y los recursos para acceder a ellos, cámara, micrófonos).   Respeta  al docente  y a sus compañeros del grupo en el uso de la palabra o mensajes por el chat, en las sesiones de interacción por  los medios virtuales que se utilicen en las clases, evitando compartir el link con personas ajenas a la clase.  Aplica las normas establecidas en la clase de matemáticas para la buena convivencia en los encuentros virtuales.

MULTIPLICACIÓN  DIVISIÓN  Y POTENCIACIÓN DE NÚMEROS ENTEROS 

Tomado de https://es.wikibooks.org/wiki/Aritm%C3%A9tica/Multiplicacion_de_N%C3%BAmeros_Enteros

Aritmética/Multiplicacion de Números Enteros

< Aritmética

Ir a la navegaciónIr a la búsqueda

La multiplicación de números enteros, al igual que la suma, requiere determinar por separado el signo y valor absoluto del resultado.

En la multiplicación (o división) de dos números enteros se determinan el valor absoluto y el signo del resultado de la siguiente manera:

• El valor absoluto es el producto de los valores absolutos de los factores.
• El signo es «+» si los signos de los factores son iguales, y «−» si son distintos.

Para recordar el signo del resultado, también se utiliza la regla de los signos:

Definición. * (+) × (+)=(+) Más por más igual a más.

• (+) × (−)=(−) Más por menos igual a menos.
• (−) × (+)=(−) Menos por más igual a menos.
• (−) × (−)=(+) Menos por menos igual a más.

Ejemplos. (+4) × (−6) = −24 , (+5) × (+3) = +15 , (−7) × (+8) = −56 , (−9) × (−2) = +18.

La multiplicación de números enteros tiene también propiedades similares a la de números naturales:

La multiplicación de números enteros cumple las siguientes propiedades:

• Propiedad asociativa. Dados tres números enteros  los productos  son iguales.
• Propiedad conmutativa. Dados dos números enteros  los productos  son iguales.
• Elemento neutro. Todos los números enteros quedan inalterados al multiplicarlos por 1: 

Ejemplo.

1. Propiedad asociativa:

1. [ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140

   (−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140

2. Propiedad conmutativa:

   (−6) × (+9) = −54

   (+9) × (−6) = −54

La suma y multiplicación de números enteros están relacionadas, al igual que los números naturales, por la propiedad distributiva:

Propiedad distributiva.' Dados tres números enteros , el producto  y la suma de productos  son idénticos.

Ejemplo.

• (−7) × [ (−2) + (+5) ] = (−7) × (+3) = −21
• [ (−7) × (−2) ] + [ (−7) × (+5) ] = (+14) + (−35) = −21

VIDEO TUTORIAL1  JULIO PROFE : Multiplicación y división de números enteros.

VIDEO TUTORIAL2: RUBÉN SEBASTIAN:  Operaciones combinadas

POTENCIACIÓN  DE  NÚMEROS ENTEROS

Tomado de: https://sites.google.com/site/angelpuente/los-numeros-enteros/3-14---potencia-de-numeros-enteros

3. Los Números Enteros‎ > ‎

3.14.- Potencia de números enteros

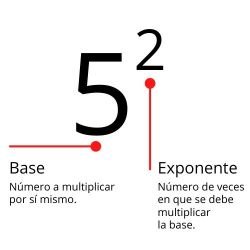
1.- BASE POSITIVA Y EXPONENTE POSITIVO Ya lo hemos visto puesto que coincide con las potencias de números naturales. 2.- BASE NEGATIVA Y EXPONENTE POSITIVO No hay ninguna dificultad. Únicamente debemos tener cuidado al multiplicar los signos negativos. (− 2)1 = − 2 (− 2)2 = (− 2) ⋅ (− 2) = 4 (− 2)3 = (− 2) ⋅ (− 2) ⋅ (− 2) = − 8 (− 2)4 = (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) = 16 (− 2)5 = (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) ⋅ (− 2) = − 32 Regla de los signos: Cuando la base es negativa y el exponente es par el resultado es positivo. Cuando la base es negativa y el exponente es impar el resultado es negativo. 3.- BASE POSITIVA Y EXPONENTE NEGATIVO De acuerdo con la definición inicial de potencia: 4(–3) consistiría en realizar una multiplicación de 4 por sí mismo tantas veces como diga elexponente, en este caso, –3. Esto, lógicamente, no tiene sentido. En cambio, los matemáticos se han puesto de acuerdo en darle un significado a esta expresión: En general: Para explicar este resultado acudimos a la fórmula de la división de potencias de la misma base: Pero esto se puede resolver realizando las potencias por separado y simplificando: Así, para que la fórmula de la división de potencias funcione siempre, se acordó que la potencia de exponente negativo es igual a 1 dividido por la misma potencia pero elevada a exponente positivo. 4.- BASE NEGATIVA Y EXPONENTE NEGATIVO Es parecido al caso anterior pero ahora la base sigue siendo negativa: 5.- BASE POSITIVA O NEGATIVA Y EXPONENTE CERO Cualquier número positivo o negativo elevado a exponente 0 es igual a 1. a0 =1 (− a)0 =1 La justificación de estos resultado se hace a partir de la división de potencias de la misma base: 32 : 32 = 30 Pero también se puede resolver realizando previamente las potencias 32 : 32 = 9 : 9 = 1 Lo mismo ocurre cuando las bases son negativas: (−2)3 : (−2)3 = (−2)0 (−2)3 : (−2)3 = (−8) : ( −8) = 1 Tomado de https://www.significados.com/leyes-de-los-exponentes/ ¿Cuáles son las leyes de los exponentes? Las leyes de los exponentes son el conjunto de reglas establecidas para resolver las operaciones matemáticas con potencias. La potencia o potenciación consiste en la multiplicación de un número por sí mismo varias veces, y se representan gráficamente de la siguiente manera: xy. El número que se ha de multiplicar por sí mismo es llamado base y el número de veces por el que se ha de multiplicar es llamado exponente, el cual es más pequeño y debe situarse a la derecha y arriba de la base. 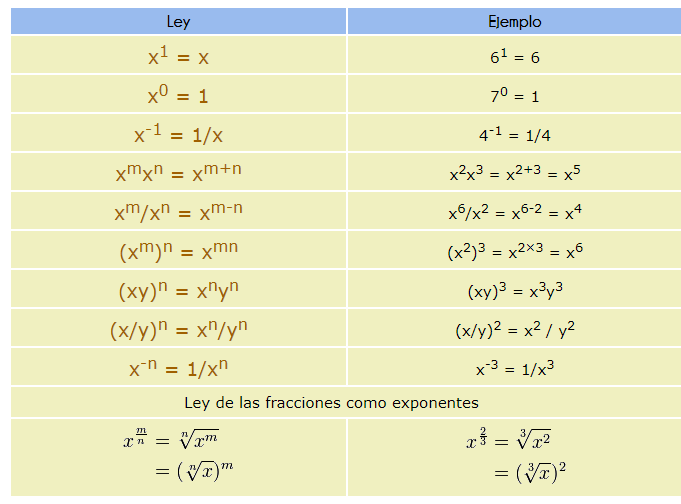Por ejemplo, Ahora bien, en operaciones de suma, resta, multiplicación y división con una o varias potencias, ¿cómo proceder? Las leyes de los exponentes nos guían para resolver estas operaciones de la manera más simple posible. Veamos. 1) Potencia cero 1) Todo número elevado a la 0 es igual a 1. Por ejemplo, x0 = 1 50 = 1 370 = 1 2) Potencia a la 1 Todo número elevado a 1 es igual a sí mismo. Por ejemplo, x1 = x 301 = 30 451 = 45 3) Multiplicación de potencias con la misma base El producto de potencias con base idéntica es igual a una potencia de igual base, elevada a la suma de los exponentes. Por ejemplo, 24 · 22 · 24 = 2(4 + 2 + 4) = 210 4) División de potencias con la misma base Cuando se dividen potencias con la misma base y exponentes diferentes, el cociente es igual a otra potencia con la misma base elevada a la suma de los exponentes. Por ejemplo, 44 : 42 = 4(4 - 2) = 42 5) Multiplicación de potencias con el mismo exponente El producto de dos o más potencias diferentes con igual exponente es igual al producto de las bases elevado al mismo exponente. Por ejemplo: 32 · 22 · 32 = (3 · 2 · 3)2 = 182 6) División de potencias con el mismo exponente El cociente entre dos potencias con base diferentes e igual exponente resulta en el cociente de las bases elevado al mismo exponente. Por ejemplo, 82 : 22 = (8 : 2)2 = 42 7) Potencia de una potencia La potencia de una potencia resulta en otra potencia con la misma base elevada al producto de los exponentes. Por ejemplo: (83)3 = 8(3 · 3) = 89 También te puede interesar Leyes de los exponentes y los radicales.

EJERCICIOS DE APLICACIÓN

Tomado de  https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/racionales/ejercicios-resueltos-de-potencias.html

Ejercicio 1

Escribe en forma de una sola potencia: Aplicando la Ley de exponentes y escribe el nombre de la propiedad empleada en cada ejercicio.

 

1 3³ · 3⁴ · 3 =                           2 5⁷ : 5³ =                         3 (5³)⁴ =             

 

4 (5 · 2 · 3)⁴ =                          5 (3⁴)⁴ =                            6 [(5³)⁴]² =

 

7 (8²)³=                                     8 (9³)²=                              9 2⁵ · 2⁴ · 2 =

 

10 2⁷ : 2⁶ =                               11 (2²)⁴ =                           12 (4 · 2 · 3)⁴ =

 

13 (2⁵)⁴ =                                   14 [(2³)⁴]⁰=                        15 (27²)⁵=

 

16 (4³)² =

 

Ejercicio 2

Realizar las siguientes operaciones con potencias:

1 (−2)² · (−2)³ · (−2)⁴ =                     2 (−8) · (−2)² · (−2)⁰ (−2) =    

3 (−2)⁻² · (−2)³ · .(−2)⁴ =                   4 2⁻² · 2⁻³ · 2⁴ =

 5 2² : 2³ =                                         6 2⁻² : 2³ =

7 2² : 2⁻³ =                                          8 2⁻² : 2⁻³⁼

9 [(−2)⁻²] ³ · (−2)³ · (−2)⁴ =                   10 [(−2)⁶ : (−2)³]³ · (−2) · (−2)⁻⁴ =

 

 

Ejercicio 3